ゲームが強くなりたい、というのはある程度ゲームに慣れ親しんでいる人ならまあまあ誰しも抱く願望です。
ゲームによっては最初からある程度強力なコンピューターが用意されていますし、今時は機械学習という強力なツールにより、どんな種類のゲームでも人間を凌駕する実力を手に入れたAIを作ることはかなり容易になってきています。

もちろん、機械学習や強化学習という言葉は聞いたことがあっても、まだあまり具体的なイメージができていない人がほとんどでしょう。私もそこまではっきりとイメージができていなかったのですが、アナログゲームの一研究家として、いつかは通らなければならない道だろうなとはずっと思っていました。今回は、実際に素人が強化学習でゲームを「正しく」プレイできるAIを作ってみます。
素人がほんの興味程度でいきなりググっても複雑怪奇な数式ばかりで一瞬で心を折られる分野ですが、このページでは前知識のない人がなんとか雰囲気だけでもわかってもらえるよう、極力やさしい表現で説明しています。
強化学習には様々な手法がありますが、ここでは最も基本的な手法のひとつであるQ学習というものを扱います。
Contents
Q学習とは?
Q学習は強化学習の手法のひとつで、基本的かつ最もよく知られているもののひとつです。
状態 \(s\) で行動 \(a\) を取ったときに報酬 \(r\) が得られて状態が \(s’\) に遷移したとき、\(Q\)テーブルの値を以下の式で更新します。
$$Q(s, a) \leftarrow Q(s, a) + \eta (r+\gamma\,\underset{a’}{max}\,Q(s’, a’)\,-\,Q(s, a)) \\ (=(1-\eta)Q(s, a) + \eta (r+\gamma\,\underset{a’}{max}\,Q(s’, a’)))$$
え、何???
いちから丁寧に説明する

まあ専門家の皆さんが専門用語山盛りでおしゃべりするのは必要悪みたいなところがあるんですけど、我々はそんな難しいことはわからないので、簡単な言葉で説明しましょう。
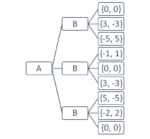
まず\(Q(s,a)\)というのは、\(s\)という状態でプレイヤーが\(a\)という行動を取った時の価値を表す関数です。関数と言っても中学生がやる数学のように何か計算式があるわけではなく、単純に「状態と行動」と「価値」が一対一対応しているだけのものです。Qテーブルというのはこれを集積したものです。
AIくんは最初は何も知らない状態から始めるので、どんな\(s, a\)の組に対しても\(Q(s,a) = 0\)だと思っています。
でも実際にランダムに○や×を置いてみると、そんなことはないなとわかってきます。
ルールの情報などは特に与えず、結果に応じてAIくんに報酬を与えます。今回は○か×を置いた瞬間に勝利条件を満たしたら、10円の報酬をあげることにしましょう。
ちなみに途中経過でできる特定の盤面に対しては特別な報酬はあげません。たとえば三目並べならダブルリーチの状況を作って勝ち確定の盤面を作ることができますが、それに対して特別に報酬をあげるようなことはしません。その辺は勝手に学習してくれるからです。あくまで実際に勝ちになった時にのみ大きな報酬をあげます。
AIくんは報酬をもらったら、それを基に学習を行い、その結果をQテーブルに反映させます。
ランダムに試行した結果○が勝ったとしましょう。そうすると、直接的に勝ちになる手には、○の立場からすると単純に10円の価値がある、ということになります。
その直前の手、×を置いた手は、負けに繋がってしまったので、×の立場からするとおそらくかなり価値が低いだろう、と考えます。さらにその前の○を置いた手は遠回しに勝ちにつながっているので、10円ほどではないがちょっと価値がある手だったのだろう、という感じで、遡って学習するのです。
AIくんはこれを何度も繰り返します。人間だと数回か数十回程度ゲームを繰り返すことでなんとなく傾向を掴みますが、機械学習の場合はこれが万や億、場合によってはそれ以上の単位に及びます。今回は簡単なゲームなので、とりあえず100万回試行して学習させてみます。1回のゲームを一瞬(1ミリ秒未満!)で終わらせてしまうコンピューターならではの方法です。
高校数学までの知識で式を解釈する
さて、さっき上で書いた一見めちゃくちゃな式ですが、これは一体どういう意味だったのでしょうか?
$$Q(s, a) \leftarrow Q(s, a) + \eta (r+\gamma\,\underset{a’}{max}\,Q(s’, a’)\,-\,Q(s, a)) \\ (=(1-\eta)Q(s, a) + \eta (r+\gamma\,\underset{a’}{max}\,Q(s’, a’)))$$
まず、全く解説してもいないのに唐突に出てきている変数について確認しましょう。
\(\eta\,=\) 学習率
\(\eta\) は学習率というパラメータです。直近の試行の結果をどの程度評価に反映させるかを表します。
基本的に、\(0<\eta\leq1\) の値を取ります。\(\eta=0\) にするとまるで学習しませんので強化学習になりません。また \(\eta=1\) にすると最後の試行が全てだと思って(仮にそれが偶然の産物で間違っていたとしても)今までの結果を全て放り出してしまう単細胞になってしまうので通常そのようなことはしません。
\(\gamma\,=\) 割引率
お得そうなワードが出てきましたが夕方のスーパーのお総菜売り場ではありません。これは将来得られるであろう報酬をどれくらい重視するかというパラメータです。
これも基本的には、\(0\leq\gamma\leq1\) の値を取ります。\(\gamma=0\) にすると目の前の報酬にしか興味を示さなくなります(一手先を全く考慮しなくなる)。\(\gamma=1\) にすると先々の報酬を今すぐ得られる報酬と同等に扱います。実際には0.95や0.99など、1に近い値を使うことが多いようですが、どれくらいの値が最適であるかというのははっきりしていません。ゲームの種類にもよるようです。
\(\underset{a’}{max}\,Q(s’, a’)\,\text{≒}\) 想定される次の手の価値
このカタマリですが、全部まとめて「次の手として想定される全ての手のうち、最も価値が高い手の価値」を表しています。有限個の選択肢を提示されたら一番価値が高い手を選ぶだろう、という楽観的な予測をするわけです。実際勝とうと思ったらそのような選択をするわけですから、これは理に適っていると言えます。
迷路などの1人用のゲームでは常にこの値が高くなるように考えれば良いですが、○×ゲームの場合は一手ごとに手番が入れ替わるため、相手にとって最も価値が高い手=自分にとって最も価値が低い手を選ぶ、という考え方になります。
等式変形?
よく見れば等式変形自体はわかってもらえると思います(文字がごちゃごちゃしているので難しく感じてしまいますが、最後の\(-Q(s,a)\)をカッコの外に出しただけです)。ここからちょっとだけ難しい話をしますが、がんばってついてきてください。
\(T = r+\gamma\,\underset{a’}{max}\,Q(s’, a’)\)とします。すると、上記の式は以下のように変形できます。
$$Q(s, a) \leftarrow (1-\eta)Q(s, a) + \eta\,T$$
※左矢印は「(左辺)に(右辺)を代入する」という意味です。
ここで、\(Q\)テーブルを無限回更新する想定で、以下のような漸化式を考えます。
$$q_{n+1}=(1-\eta)q_n + \eta\,T\\(0<\eta\leq1)$$
\(T\) が \(n\) の値によらない定数なら、この漸化式は $$\displaystyle\lim_{n \to \infty} q_n = T$$ なので、\(T\)に収束します。この「評価値が一定の値に収束することが担保されている」という性質が強化学習の信頼性の根拠です。
実装してみる
機械学習といえばpythonですが、私が個人的に使い慣れているのと、遊ぶためのUIの作りやすさを優先して、C#を使ってプログラムを書いていきます。
これだけあっても動かないんですが強化学習の部分だけソースコードを載せておきます↓
解説はここではしませんので、わからない部分などありましたらメール等で個別にご質問ください。
using System;
using System.Collections.Generic;
using TicTacToeLearning.mainsource.gamestructure.template;
namespace TicTacToeLearning.mainsource.gamelearning {
internal class SingleRun {
IStructure structure;
public Nodes nodes;
private Random random;
private double epsilon = 0.1d; //戦略乱数
private double eta = 0.1d; //学習率
private double gamma = 0.9d; //割引率
private List<int> history = new List<int>();
public SingleRun(IStructure structure): this(structure, 0.1d, 0.1d, 0.9d) {
}
public SingleRun(IStructure structure, double epsilon, double eta, double gamma) {
this.structure = structure;
this.epsilon = epsilon;
this.eta = eta;
this.gamma = gamma;
nodes = new Nodes(structure);
random = new Random();
nodes.OverwriteNodeVal(0, 0);
}
public Dictionary<int, double> GetNodes() {
return nodes.GetNodes();
}
public void RunAIvsAIStudy() {
int board = structure.Initialize();
bool isFirstP = true;
history.Clear();
do {
int recommend = nodes.SearchNodeWithMaxValue(board, isFirstP);
if (random.NextDouble() >= epsilon) {
board = recommend;
} else {
int[] i = nodes.FindNextNode(board, isFirstP);
board = i[random.Next(0, i.Length)];
}
history.Add(board);
isFirstP = !isFirstP;
} while (nodes.FindNextNode(board, isFirstP).Length != 0 && structure.IsWin(board) == 0);
int terminal = history[history.Count - 1];
int reward = structure.IsWin(terminal);
nodes.OverwriteNodeVal(terminal, reward * 9);
for (int i = 1; i < history.Count; i++) {
int n = history[history.Count - i - 1];
double nodeVal = nodes.GetNodesValue(n) + eta * (reward
+ gamma * nodes.GetNodesValue(nodes.SearchNodeWithMaxValue(n, (history.Count - i - 1) % 2 == 1))
- nodes.GetNodesValue(n));
nodes.OverwriteNodeVal(n, nodeVal);
}
}
}
}
using System.Collections.Generic;
using TicTacToeLearning.mainsource.gamestructure.template;
namespace TicTacToeLearning.mainsource.gamelearning {
internal class Nodes {
IStructure structure;
private Dictionary<int, double> nodes;
private Dictionary<int, int[]> nextNodes;
public Nodes(IStructure structure) {
this.structure = structure;
nodes = new Dictionary<int, double>();
nextNodes = new Dictionary<int, int[]>();
}
public void OverwriteNodeVal(int node, double value) {
nodes[node] = value;
}
public double GetNodesValue(int node) {
return nodes[node];
}
public Dictionary<int, double> GetNodes() {
return nodes;
}
public int[] FindNextNode(int node, bool first) {
if (nextNodes.ContainsKey(node)) {
return nextNodes[node];
} else {
nextNodes[node] = structure.ListingLegalMove(node, first);
foreach(int i in nextNodes[node]) {
if (!nodes.ContainsKey(i)) {
nodes.Add(i, 0);
}
}
return nextNodes[node];
}
}
public int SearchNodeWithMaxValue(int node, bool positive) {
int returnNode = 0;
double returnNodeVal = positive ? double.MinValue : double.MaxValue;
foreach (int nextNode in FindNextNode(node, positive)) {
if ((positive && nodes[nextNode] > returnNodeVal) || (!positive && nodes[nextNode] < returnNodeVal)) {
returnNode = nextNode;
returnNodeVal = nodes[nextNode];
}
}
return returnNode;
}
public bool IsTerminalNode(int node, bool first) {
return FindNextNode(node, first).Length == 0 || structure.IsWin(node) != 0;
}
public bool IsTerminalNode(int node) {
return (FindNextNode(node, true).Length == 0 && FindNextNode(node, false).Length == 0) || structure.IsWin(node) != 0;
}
}
}
【余談】ハードコーディングしないでおく
ちょっと手間ではあるのですが、ここで「強化学習をするためのプログラム」と「○×ゲームを定義するプログラム」は明確に分けて書いておきます。
ハードコーディングとは?
プログラムを開発する時、ある特定の動作環境を決め打ちして、コードを書くことを「ハードコーディング」と言います。この場合だと、このプログラムを○×ゲーム専用に書いてしまうことをそのように呼びます。
上で載せておいたソースコードには、○×ゲームの定義に関する内容は一切含まれていません。その情報は別に記述して、実行時に読み込ませています。
ゲームの定義と機械学習の根幹を分けることで、たとえば盤面が広がったらどうなるのかとか、四目並べならどうなのかとか、そういう解析にも使うことができるようになります。
これが次回以降の大切な伏線になります。
実際に動かしてみる
実際に実装してみた画面を見てみましょう。学習を100万回繰り返すと、以下のようになります。

学習にかかった時間は2.638秒/100万回です。
左上の数字はそこに置く手の価値を示しています。プラスの数値は○有利、マイナスの数値は×有利であることを表しています。これを見る限り、○は最初の手は真ん中を選ぶのが明らかに価値が高そうです。
試しに真ん中に〇を置いてみるとこうなります。

次は×の手番なので、価値がよりマイナスになるような手を選びたいです。我々は経験的に、ここで×が手を間違うと○の必勝形になるということを知っていますが、AIくんも100万回にも及ぶ試行の中でそれを理解したらしく、角のマスを選びたがっているようです。ちゃんと学習できていますね。
ここではあえて、間違った手を選んでみます。


すると○はちゃんと必勝形になるような手を取るように、正しく盤面を評価できています。えらいね~!
三目並べではないゲームに応用してみる
さて、これがたとえば盤面が4×4の4目並べだったらどうなるでしょう? 人間の目には明らかに引き分けだと分かりますが、AIくんは正しく見抜けるでしょうか。
ゲームの構造を定義するプログラムの部分だけを修正して、改めて動かしてみます。

おっと、重いぞ。

14秒もかかってしまいました。盤面のマスの数は倍にもなっていないのに、処理時間は5倍以上です。これはどういうことなのでしょうか?
3×3の盤面は、各マスが○か×か空白かの3通りしかないと考えると、対称性などを一切考慮しなくても高々 \(3^9=19683\) 通りしか盤面の状態がありません。この程度の計算であればコンピューターは難なくこなします。ところが、4×4に拡張するとこれが \(3^{16}=43046721\) 通りにもなります。逆によく5倍で済んだねって感じです。まあ対称性を考慮して最適化すればもっと状態数は少なくて済みますし、昨今のコンピューターの処理能力を考えれば \(10^7\) 程度のデータサイズは実は大したことはないのですが、これ以上の大きさの盤面であったり、ルールが複雑化したりすると途方もない組み合わせ数になり、爆発的に計算に時間がかかるようになる(あるいは、現実的な時間で計算不能になる)ということがわかって頂けるかと思います。
次回への伏線
さて、今回AIくんを作ってこんな遊びをしたのはもちろん理由あってのことです。
当サイトではいろんなボードゲームを遊んでレビューしているわけですが……。