最終更新日が2023年以前の記事です。レイアウト変更のため、正常に表示されない場合があります。
デルタスワップでググるとほぼ金融の話しか出てこないんですが、これは金利の話じゃないです。
デルタスワップとは
デルタスワップとは、ビット列の非連続な部分列同士を入れ替える計算、もしくはそのアルゴリズムのことです。
これだけだとわかりづらいですが、具体的には以下のような入れ替えをするのに使えます。
- 010011101010 → 101011100100 (1~4桁目と9~12桁目を入れ替え)
- 1011100100110 → 1010000111110 (入れ替える部分列は先頭や末尾でなくてもよい)
- 00110011101101 → 10011000111011 (形が同じであれば連続でなくてもよい)
こんなことして何の得になるの?と思う人と、まさにこれを求めていたんだ!と思う人がいるでしょう。
実装
ここではまるっとコピペしてそのまま使えるstaticなコードを示します。必要なimportなどは別途書いてください。
Java
public static T deltaSwap<T extends Comparable<T>>(T source, T mask, int shift){
T t = ((source >> shift) ^ source) & mask;
return source ^ (t ^ (t << shift));
}動かなければextends Comparable<T>の部分を消してください。
JavaScript
function delta_swap(source, mask, shift){
let t = ((source >> shift) ^ source) & mask;
return source ^ (t ^ (t << shift));
}C#
public static T DeltaSwap<T>(T source, T mask, int shift) where T : struct {
T t = ((source >> shift) ^ source) & mask;
return source ^ (t ^ (t << shift));
}動かなければwhere T : structの部分を消してください。
各引数の意味
- source : 変換したい値。
- mask : 入れ替えたい桁同士のうち、より小さい位にある桁に1を立てたバイナリデータ
- shift : 入れ替えたい桁同士の距離。
たとえば、010011101010 → 101011100100の変換であれば、
source = 0b010011101010mask = 0b000000001111shift = 8
となります。
アルゴリズムの中身
このアルゴリズムで使う論理演算子はANDとXORだけですが、XORについての以下の性質を把握しておくとこの後の理解がスムーズです。
$$A\,\oplus\,B\,\oplus\,B\,= A\\ (A\,{\rm xor}\,B\,{\rm xor}\,B\,= A)$$
同じ値を2回XOR演算すると、元の値に戻ります。
$$A\,\oplus\,A\,\oplus\,B\,= B\\ (A\,{\rm xor}\,A\,{\rm xor}\,B\,= B)$$
ある値 \(A\) に対して \(A\) と \(B\) をXOR演算すると、\(B\) になります。
一見当たり前のようですがこれが重要です。
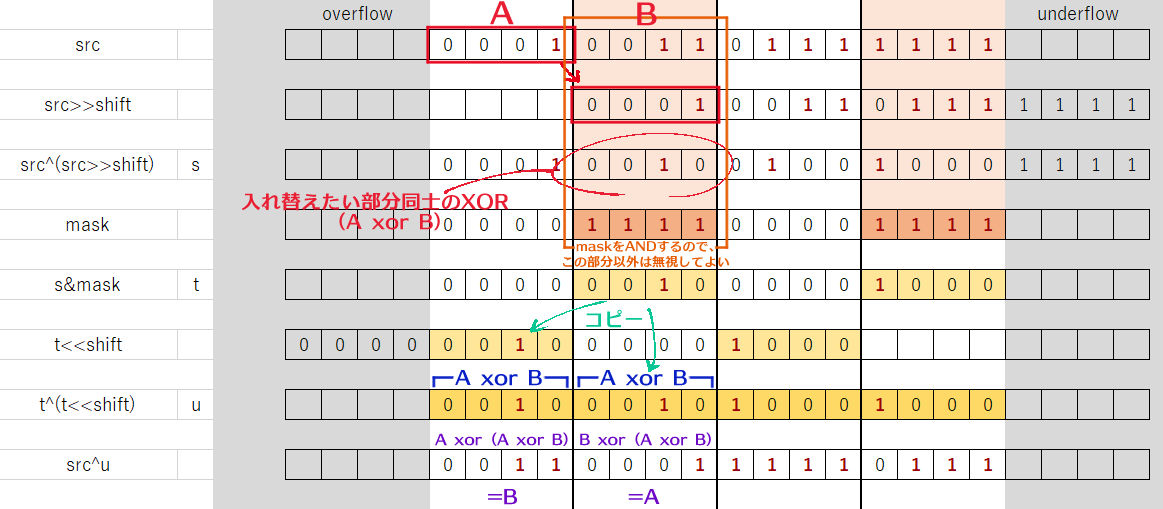
ぱっと見て何をやっているかを理解できるほど賢い人はそうそういないと思うので(私もわかりませんでした)、一個ずつ順を追って計算してみました。流れは以下の通りです。
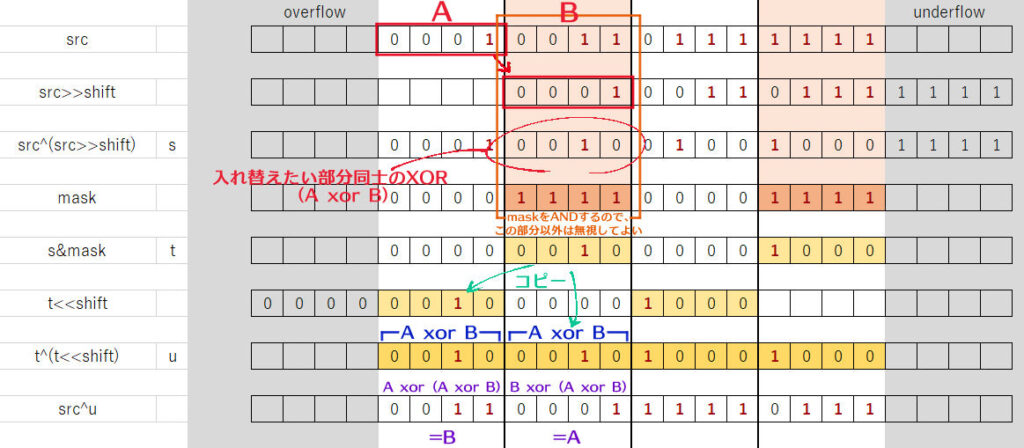
入れ替えたい部分同士のXORを作って、入れ替えたい部分にXOR演算すると、\(A\,{\rm xor}\,A\,{\rm xor}\,B\,= B\) になることを利用して値を入れ替えることができる、というわけです。なるほどね。
応用(これって何に使うの?)
これを使ってできることは色々ありますが、たとえばひっくり返したビット列を高速に得られます。
11110111011010 → 01011011101111
これのことをビット反転と呼ぶか呼ばないかは専門家ではないのでわからないのですが、英語ではbit reverse(ビットリバース)と呼ぶみたいです。
一般的に日本語でビット反転というとbit not か bit flipのことを指すようです(0010→1101のような)。
\(n\)桁のビット列をリバースするのに必要な計算量を考えると、愚直に実装するなら左から\(x\)番目と右から\(x\)番目を入れ替え、を\(n/2\)回繰り返すので、計算量は\(O(n)\)ですが、デルタスワップを使うとこれが\(O(\log{n})\)になります。なんで?
実際に32bitの値に対してビットリバースした値を求める関数を書くと以下のようになります(以下はJavaの例です)。
public static int int32rev(int source){
source = deltaSwap<int>(source, 0b01010101010101010101010101010101, 1);
source = deltaSwap<int>(source, 0b00110011001100110011001100110011, 2);
source = deltaSwap<int>(source, 0b00001111000011110000111100001111, 4);
source = deltaSwap<int>(source, 0b00000000111111110000000011111111, 8);
return deltaSwap<int>(source, 0b00000000000000001111111111111111, 16);
/* ここではぱっと見てわかりやすくするため2進数で書きましたが、
普通は16進表記で書くことが多いです。その場合、上から順に
0x55555555
0x33333333
0x0f0f0f0f
0x00ff00ff
0x0000ffff
となります。*/
}まとめて複数の桁を入れ替える操作が計算量1でできるというのを上手く利用した例ですね。